[알고리즘] Dynamic Programming

개요

최적화 이론의 한 기술이며, 특정 범위까지의 값을 구하기 위해서 그것과 다른 범위까지의 값을 이용하여 효율적으로 값을 구하는 알고리즘 설계 기법입니다. 즉 작은 문제를 해결한 후, 해결한 작은 문제의 해답을 활용하여 주어진 문제들을 풀어 최적화하여 풀면

---

설명

주어진 문제를 풀기 위해서, 문제를 여러 개의 하위 문제(subproblem)로 나누어 푼 다음, 그것을 결합하여 최종적인 목적에 도달하는 것입니다. 각 하위 문제의 해결을 계산한 뒤, 그 해결책을 저장하여 후에 같은 하위 문제가 나왔을 경우 그것을 간단하게 해결할 수 있습니다. 이러한 방법으로 동적 계획법은 계산 횟수를 줄일 수 있습니다. 특히 이 방법은 하위 문제의 수가 기하급수적으로 증가할 때 유용합니다.

Dynamic Programming 활용

type1 -> Top-down

https://hien-luu.medium.com/dissecting-dynamic-programming-top-down-bottom-up-3d3a1d62fbd7

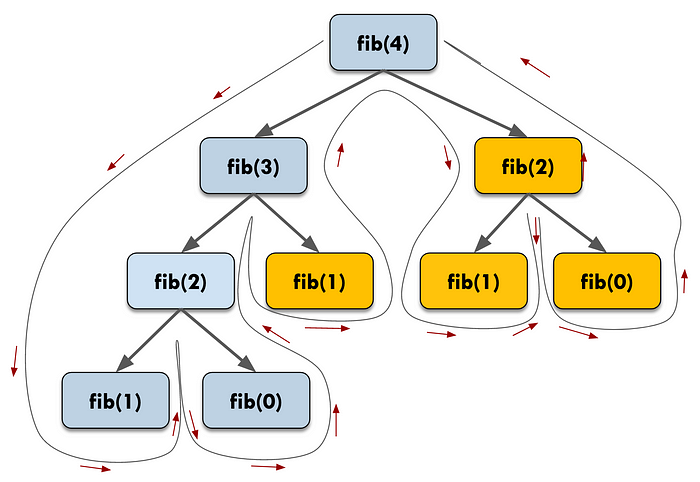
val arr_dp_topdown = IntArray(46) { 0 }
fun fibonacci_topdown(i: Int): Int {
    if (i <= 1) return i
    if (arr_dp_topdown[i] == 0) arr_dp_topdown[i] = fibonacci_topdown(i - 1) + fibonacci_topdown(i - 2)
    return arr_dp_topdown[i]
}

이렇게 되면 해당 함수를 2번 이상 사용할 경우 값이 이미 저장되어 있기 때문에 더욱 빨리 풀 수 있습니다. 그렇지만 처음 풀이 때는 중복연산을 해야 합니다

---

type2 -> Bottom-up

https://www.interviewbit.com/courses/programming/dynamic-programming/dynamic-programming-methods/

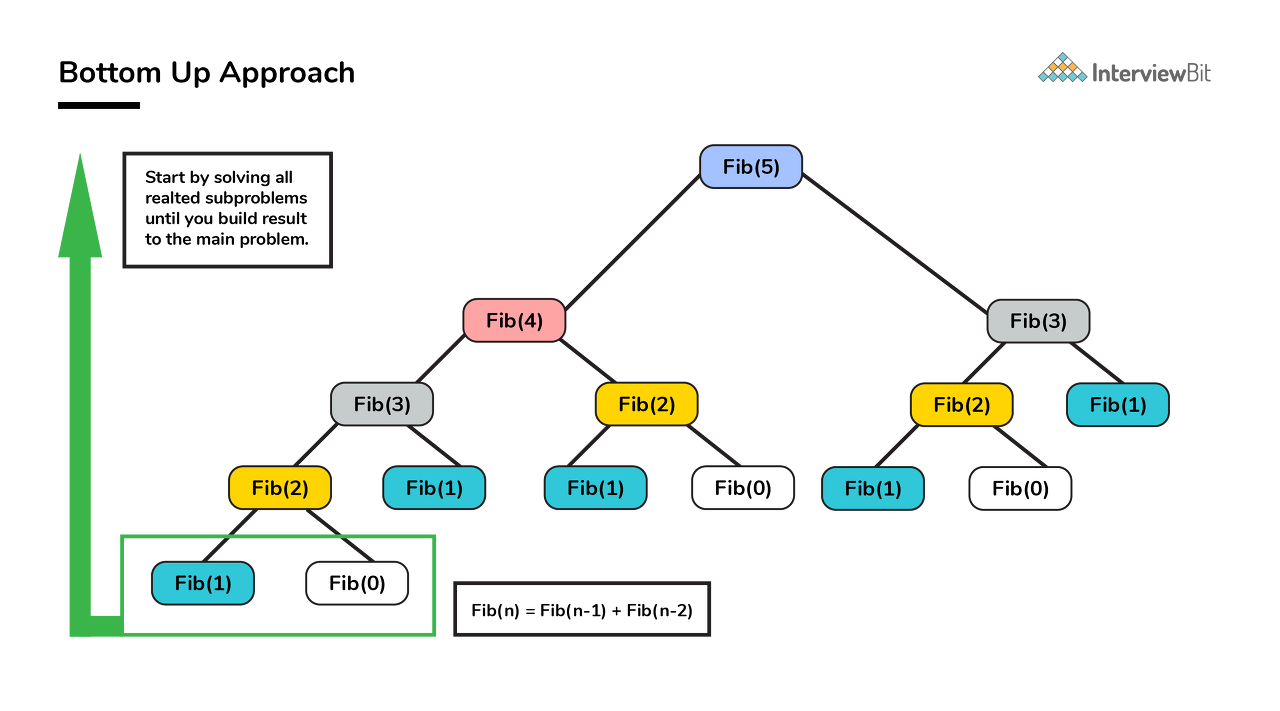
val arr_dp_bottomup = IntArray(46) { 0 }
var last_pos = 1
fun fibonacci_bottomup(i: Int): Int {
    if (i <= 1) return i
    if (arr_dp_bottomup[i] == 0){
        for (j in last_pos .. i){
            arr_dp_bottomup[j] = arr_dp_bottomup[j-1] + arr_dp_bottomup[j-2]
        }
        last_pos = i + 1
    }
    return arr_dp_bottomup[i]
}

이경우에는 밑에서부터 값을 넣어주기때문에 불필요한 연산을 할 필요가 없어집니다

---

참고

https://namu.wiki/w/%EB%8F%99%EC%A0%81%20%EA%B3%84%ED%9A%8D%EB%B2%95

동적 계획법 - 나무위키

 

https://ko.wikipedia.org/wiki/%EB%8F%99%EC%A0%81_%EA%B3%84%ED%9A%8D%EB%B2%95

동적 계획법 - 위키백과, 우리 모두의 백과사전